游戏开发基础图形学基础

图形学知识是基础，即便你在使用的游戏引擎已经帮你完成了大多数工作，但是这些基础的概念有助于你对渲染的过程有更好的理解，才会知其所以然。所以趁着复习的机会在这里整理一些必要的知识基础。

图形管线

图形管线概述

图形管线，这是绝大多数计算机渲染的基础过程。渲染管线其实并不是一个很高深的名词，也有的人会叫做图形学管线、GPU渲染管线等，只是表示计算机如何把图形图像信息显示到你的屏幕上来这一过程，因为类似于工厂的流水线，所以才叫管线。

图形管线要把模型转换成屏幕画面的过程，由于这个过程中所进行的操作严重依赖用户所使用的软件、硬件等，因此并不存在通用的绘图流水线。尽管如此，现今存在着类似Vulkan、OpenGL和DirectX的图形接口，将相似的操作统一起来，并把底层硬件抽象化，以减轻程序员的负担，逐渐成为最为主流的图形接口。

泛化的来讲，图形管线在概念上一般分为3大阶段：

应用阶段(Application): 主要在CPU中进行，将所有图元（通常是三角形、线和点）传递到GPU的渲染管线，除此之外还有一些空间细分、碰撞检测、动画、变形都在此阶段进行，这些有助于减少内存使用。
几何阶段(Geometry): 主要负责对输入的几何数据进行处理和转换。包括顶点着色器（Vertex Shader），它对输入的顶点进行变换和处理，例如执行模型变换、视图变换和投影变换等；还包括曲面细分（Tessellation）和几何着色器（Geometry Shader）等。
光栅化阶段(Rasterization): 在这个阶段，几何数据被转换为屏幕上的像素片段。它将几何图形（如三角形）转换为像素片段，并确定每个像素片段的位置、颜色和其他属性

有很多文章中会分为4个阶段，除了上述的三个阶段外还会有：

像素处理阶段(Pixel): 该阶段对最终的像素进行处理和操作。包括混合（将多个像素的颜色进行混合）、深度测试（根据像素的深度值进行可见性判断）以及模板测试（根据像素的模板值进行特定操作）等

这是因为以前的老显卡仍然比较接近上述的图形管线。随着对GPU的需求不断增加，限制逐渐被消除，以创造更多的灵活性。现代显卡使用可自由编程、着色器控制的管道，允许直接访问各个处理步骤。为了减轻主处理器的负担，额外的处理步骤已移至管线和GPU。

不过一般面试的时候你说只有三个阶段的话，面试官可能会觉得你一知半解，恰恰是第四阶段的深度测试、模板测试之类的会是高频考点 XD

下面详细展开说一下各阶段的主要内容

各阶段主要内容

应用阶段：
在CPU上执行，顾名思义，主要是将软件层面控制的一些工作的内容应用到需要渲染的图元。更通俗的来说就是在GPU绘制之前，告诉它你要画什么。主要内容是：视锥剔除以找到可能需要绘制的图元，生成渲染数据，设置渲染状态，绑定着色器参数，最后CallDraw呼叫GPU进行下一阶段。
顺带一提，DrawCall是不是很熟悉(Unity优化时常见的术语), 为什么减少DrawCall可以提高游戏性能，原因就是：CPU频繁的调用GPU的绘画，每次都只提交很少的绘画内容，虽然CPU的计算很快，但是CPU频繁的DrawCall使得CPU的效率低下。
对于GPU而言, GPU的绘画速度远远快于CPU提交的速度，CPU成为了GPU的负担，而使用一些合批手段，尽量让CPU减少提交的次数，提高每次提高的内容，尽量减小CPU进行提交遇到的瓶颈*。这不就是融会贯通了吗。
几何合阶段： 几何阶段在GPU上运行，它处理应用阶段发送的渲染图元，负责大部分的逐三角性和逐顶点操作。几何阶段的一个重要任务就是把顶点坐标变换到屏幕空间中，再交给光栅器进行处理。主要有以下几个阶段：顶点着色、投影、裁剪、屏幕映射：
1. 顶点着色： 计算顶点位置，顶点从模型空间通过MVP转换到了齐次裁剪空间。MVP变换不展开说了(其实是我也懒得看了)，不同图形接口的MVP不太一样。
  这里还会发生一件很重要的可选项：顶点着色，Unity Shader里面的Vertex Shader就是在这里处理的。这个阶段是完全可控制的，取决于你的Shader是怎么写的。（比如写一个草丛的Shader，顶点位置会周期性的摆动等） 此外，在顶点处理阶段的末尾，还有一些可选的阶段，包括曲面细分(tessellation)、几何着色(geometry shading)和流输出(stream output)，此处不详细描述
2. 裁剪阶段： 对部分不在视体内部的图元进行裁剪。这部分是几乎完全由硬件控制的，因此没必要详细描述。这里的裁剪不同于剔除，剔除是决定图元需不需要渲染，而NDC裁剪在这里是将图元裁剪，这会减少部分像素处理的工作，如下图所示(值得注意的是，真实的渲染管线要复杂得多，这里只是说个大概意思)：
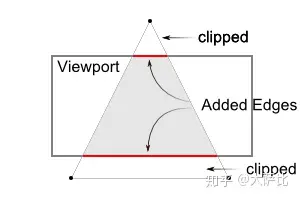
1. 屏幕映射： 主要将之前步骤得到的坐标映射到屏幕坐标系。
光栅化阶段： 光栅化阶段的目标是找到处于图元(三角形)内部的所有像素，进而将2D坐标顶点转为屏幕上的像素，每个像素附带深度和其他着色信息，它们一并传入pixel。光栅化阶段分为两个完全由硬件控制的子阶段：
1. 三角形设置(Triangle Setup)(图元装配): 计算出三角形的一些基本数据(如三条边的方程、深度值等)以供三角形遍历阶段使用。
2. 三角形遍历(Triangle Traversal): 找到哪些像素被三角形所覆盖，并对这些像素的属性值进行插值。通过判断像素的中心采样点是否被三角形覆盖来决定该像素是否要生成片段。通过三角形三个顶点的属性数据，插值得到每个像素的属性值。此外透视校正插值也在这个阶段执行。
像素处理阶段： 它主要处理光栅化阶段发送过来的在图元内部的片元序列。GPU会对每个片元进行像素操作，如颜色和深度的计算、纹理采样、混合等。主要分为两大阶段：
1. 像素着色：使用光栅化阶段传递的插值后的数据以及纹理计算像素颜色，进行光照计算和阴影处理，决定屏幕像素的最终颜色
  需要注意的是，纹理可以认为是一种独立于”插值“数据的一种资源。由于顶点和像素着色器一般数据都存在更小更快的L1缓存(L1 Cache)中，但纹理存储在更大更慢的L2缓存(L2 Cache)中，因此纹理访问是有延迟的，线程先执行不产生延迟的指令，当遇到产生延迟的指令时，快速切换到其他片元执行其他任务并递归运行。Shader占用的寄存器越多，当内存延迟时，有可能会产生线程被迫等待的情况，这被称作占用率过高
2. 测试合并：包括各种测试和混合操作，如裁剪测试、透明测试、模板测试、深度测试以及色彩混合等。经过了测试合并阶段，并存到帧缓冲的像素值，才是最终呈现在屏幕上的图像。
  深度测试是在像素着色器之后才执行的。这种做法会导致很多不可见的像素也会执行像素着色器计算，从而浪费了计算资源。
  为了避免这种浪费，后来的GPU架构采用了Early-Z技术，将深度测试提前到像素着色器之前(如下图所示)。这样一来，Early-Z技术就可以在像素着色器之前剔除很多无效的像素，从而避免它们进入像素着色器，提高了渲染性能
  我们的屏幕显示的就是颜色缓冲区中的颜色值。但是，为了避免我们看到那些正在进行光栅化的图元，GPU会使用双重缓冲(Double Buffering) 的策略，GPU会交换后置缓冲区和前置缓冲区的内容确保用户只会看到已经渲染好的内容

引擎中的渲染(Unity3D)

这里会简单介绍一下URP或者HDRP中，延迟渲染(Deferred Rendering)和前向渲染(Forward Rendering)的内容。首先先介绍一下渲染路径(rendering Path),渲染路径类似于图形管线，是指在图形渲染中用于生成最终图像的一系列渲染步骤和算法。它决定了渲染引擎在渲染过程中的执行顺序和方式。

在实时图形渲染中，常见的渲染路径包括前向渲染、延迟渲染和**后向渲染（逆向渲染）**等。每种渲染路径都有不同的优缺点，适用于不同的应用场景。

前向渲染是一种传统的渲染技术，它按照以下步骤进行：
1. 几何处理：对场景中的几何体进行处理，包括顶点变换、三角形剔除和裁剪等操作。
2. 光栅化：将几何体转化为像素片段，生成片段的位置、颜色等数据。
3. 像素处理：对每个像素片段进行处理，包括颜色插值、纹理映射、光照计算和深度测试等操作，最终生成最终的渲染图像。
优点：简单直接，适用于小规模场景和少量光源的情况。局限：当场景中有大量复杂的几何体和光源时，前向渲染需要对每个像素片段进行完整的光照计算，导致性能开销较大。
延迟渲染是一种优化的渲染技术，它将渲染过程分为以下步骤：
1. 几何处理：与前向渲染相同，对场景中的几何体进行处理。
2. 几何缓冲：将几何体的属性（位置、法线、颜色等）存储在缓冲区中，而不进行光照计算。
3. 光照处理：对每个光源进行处理，生成光照的缓冲区，存储光照信息（如漫反射、镜面反射等）。
4. 合成阶段：通过将几何缓冲和光照缓冲结合，进行最终的像素处理，包括纹理采样、深度测试和混合等操作，生成最终的渲染图像。
优点：减少了光照计算的开销，适用于复杂场景和大量光源的情况。它可以将光照计算延迟到最后的合成阶段，避免了对每个像素片段进行重复的光照计算，从而提高了性能。

矩阵与变换

MVP

在计算机图形学中，MVP代表模型-视图-投影（Model-View-Projection），是一种常用的矩阵变换顺序。它是一种用于将三维对象从模型空间（Model Space）转换到屏幕空间（Screen Space）的变换流程。

模型变换（Model Transformation）：该变换将三维对象从其本地坐标系（模型空间）转换到世界坐标系中的合适位置和方向。这个变换通常包括平移、旋转和缩放等操作。
视图变换（View Transformation）：该变换将场景从世界坐标系转换到观察者（摄像机）的坐标系。它确定了观察者的位置和方向，使得观察者仿佛位于世界坐标系的原点，朝向z轴负方向。
投影变换（Projection Transformation）：该变换将观察空间中的三维坐标转换为屏幕空间中的二维坐标，以便最终在屏幕上进行显示。它可以是透视投影（Perspective Projection）或正交投影（Orthographic Projection），具体选择取决于应用需求。

MVP变换通常通过矩阵乘法来实现。给定一个模型的顶点坐标，它首先应用模型变换，然后是视图变换，最后是投影变换，以得到最终的屏幕坐标。

有的面试官可能喜欢考察View矩阵和Projection矩阵的推导，如果你是搞游戏引擎的，这应该是必需技能；但是你的工作内容不涉及自己实现这一部分，我认为清楚原理足矣，数学原理你搞得一清二楚，真正到了开发的环境中，最终也是一个引擎提供的现成函数，分清主次，想想引擎如何更好的为你所用更现实一些。

旋转

欧拉角、矩阵和四元数都是用于表示旋转的方法，它们各自具有不同的特点、优点和缺点。 欧拉角（Euler Angles）：欧拉角使用三个角度值来表示旋转，通常是绕固定的坐标轴进行旋转（例如绕X轴、Y轴和Z轴）。欧拉角易于理解和可视化，但存在万向锁问题（Gimbal Lock），即在某些姿态下，两个旋转轴会合并，导致失去一个自由度。此外，由于旋转顺序的不同会导致不同的结果。BTW，Unity的顺序是ZXY。

矩阵：矩阵可以使用3x3或4x4的矩阵来表示旋转变换。矩阵表示法可以避免万向锁问题，且可以直接应用于坐标变换和向量变换。然而，矩阵运算相对复杂，涉及到矩阵乘法和逆运算，计算量较大，尤其是在大规模场景中。

四元数（Quaternions）：四元数是一种扩展复数的数学工具，用于表示旋转。它通过四个实数构成，包括一个标量和一个三维向量。四元数可以避免万向锁问题，且在插值和连续旋转等方面具有优势。此外，四元数在运算时具有较高的效率，尤其是在插值和球面插值计算中。然而，四元数的数学概念对于初学者来说可能较难理解，且相对于矩阵和欧拉角，其可视化和直观性较差。

光说概念没什么感觉，举个例子：我们考虑在三维空间中绕Y轴旋转一个向量。假设我们有一个向量V = [1, 0, 0]，表示沿着X轴的单位向量。我们可以使用一个3x3的旋转矩阵来表示绕Y轴旋转的变换。对于绕Y轴旋转45度的情况:

R = | cos(45°)   0   sin(45°) |
    |    0       1       0    |
    | -sin(45°)  0   cos(45°) |

V_rotated = R * V
//结果为：
V_rotated = [0.707, 0, 0.707]

使用四元数表示旋转的情况。对于绕Y轴旋转45度的情况，我们可以使用一个四元数来表示旋转变换。旋转角度为45度的绕Y轴旋转的四元数可以表示为

q = [cos(45°/2), 0, sin(45°/2), 0]
V_quaternion = [0, 1, 0, 0]
V_rotated_quaternion = q * V_quaternion
//结果为：
V_rotated_quaternion = [0.707, 0, 0.707, 0]
V_rotated = [0.707, 0, 0.707]

齐次坐标与矩阵变换

当涉及到矩阵变换时，齐次坐标是一个非常有用的工具。齐次坐标是一种扩展的坐标系统，用于表示三维空间中的点和向量，并且可以方便地进行平移、旋转和缩放等仿射变换操作。

在齐次坐标中，一个三维点由四个分量表示，通常表示为(x, y, z, w)，其中(x, y, z)是三维空间坐标，w是齐次坐标分量。齐次坐标中的点可以通过将其除以齐次分量w来还原为三维坐标，即(x/w, y/w, z/w)。这种表示方式允许我们使用矩阵来表示一系列的仿射变换操作。

矩阵变换可以通过将变换矩阵与齐次坐标进行相乘来实现。例如，对于一个平移变换，可以构造一个平移矩阵，然后将其与齐次坐标相乘，即可得到平移后的新坐标。类似地，对于旋转和缩放等变换，也可以构造相应的变换矩阵，并将其与齐次坐标相乘来实现变换。

在进行矩阵变换时，齐次坐标的第四个分量w通常为1，这样可以确保在进行除法还原为三维坐标时，保持坐标的一致性。同时，齐次坐标还可以表示无穷远点和方向向量，通过将w设置为0或其他非零值来实现。

总而言之，齐次坐标提供了一种方便的方式来表示和处理矩阵变换，使得平移、旋转和缩放等仿射变换操作可以统一地应用于三维点和向量。通过使用齐次坐标和变换矩阵，我们可以更灵活地进行各种复杂的几何变换。

平移变换：假设有一个三维点P(x, y, z)，我们想将其沿着向量T(tx, ty, tz)进行平移。可以构造平移矩阵M，如下所示：
```
M = | 1 0 0 tx |
    | 0 1 0 ty |
    | 0 0 1 tz |
    | 0 0 0  1 |
```
然后将平移矩阵M与齐次坐标[P, 1]相乘，即可得到平移后的新坐标。
缩放变换：假设有一个三维点P(x, y, z)，我们想将其沿着不同的轴进行缩放，分别缩放因子为Sx、Sy和Sz。可以构造缩放矩阵M，如下所示：
```
M = | Sx 0 0 0 |
    | 0 Sy 0 0 |
    | 0 0 Sz 0 |
    | 0 0  0 1 |
```
然后将缩放矩阵M与齐次坐标[P, 1]相乘，即可得到缩放后的新坐标。
旋转变换：假设有一个三维点P(x, y, z)，我们想围绕一个单位向量轴A进行旋转，旋转角度为θ。可以构造旋转矩阵M，如下所示：
```
M = | R11 R12 R13  0 |
    | R21 R22 R23  0 |
    | R31 R32 R33  0 |
    |   0   0   0  1 |
```
其中，R11、R12、R13等元素是根据旋转轴和旋转角度计算得到的。然后将旋转矩阵M与齐次坐标[P, 1]相乘，即可得到旋转后的新坐标

Ref

https://en.wikipedia.org/wiki/Graphics_pipeline
https://zhuanlan.zhihu.com/p/430541328
https://zhuanlan.zhihu.com/p/627201581

作者B站视频：CyberStreamer

图形管线#

图形管线概述#

各阶段主要内容#

引擎中的渲染(Unity3D)#

矩阵与变换#

MVP#

旋转#

齐次坐标与矩阵变换#

Ref#